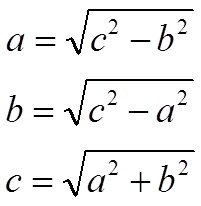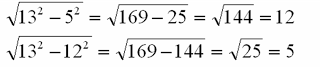Pitagora, nato a Samo intorno alla prima metà del VI secolo a.C., è una figura avvolta nella leggenda.
Il nome Pitagora significa "predetto dalla Pizia", poiché alla madre incinta fu predetto dalla Pizia, la profetessa dell'oracolo di Delfi, che avrebbe partorito un figlio sapiente. I suoi maestri furono Talete e Anassimandro.
Talete, uno dei sette saggi dell’Antichità, lo invitò a recarsi in Egitto dove avrebbe potuto incontrare altri illustri uomini di cultura. Viaggiò molto ed ampliò le sue conoscenze attingendo al sapere degli Ebrei, Fenici, Egiziani, Caldei, Persiani, Indiani. Trascorse a Babilonia molti anni e divenne esperto di astrologia e di astronomia.
Tornato a Samo, e trovata la sua patria sotto il governo del tiranno Policrate, si trasferì nella colonia di Crotone, nella Magna Grecia, e vi fondò la sua comunità.
Gli allievi erano selezionati dopo un lungo tirocinio e divisi in due categorie: gli ascoltatori ed i matematici, i quali venivano a conoscenza degli insegnamenti più elevati e dei segreti più profondi di questa società il cui simbolo era una stella a 5 punte, il pentagramma.
Nella scuola pitagorica, scienza e filosofia, musica e religione si fondevano in una mistica contemplazione dell’universo. Pitagora intuì che i numeri esistono indipendentemente dal mondo sensibile nel quale viviamo. Alla scuola pitagorica si deve la distinzione fra numeri pari e numeri dispari. Nel campo della geometria a Pitagora ed alla sua scuola viene attribuito il teorema che porta il suo nome, la risoluzione geometrica delle equazioni di secondo grado, la scoperta delle grandezze incommensurabili, i fondamenti della teoria delle proporzioni e delle similitudini.
La leggenda vuole che osservando un pavimento Pitagora ebbe una folgorazione:
Dividendo i quadrati azzurri lungo la diagonale ottieni 4 triangoli che vanno a comporre il quadrato grande.
Prima di lui, comunque, gli Egizi avevano capito che facendo un opportuno numero di nodi su una corda potevano formare un triangolo rettangolo:
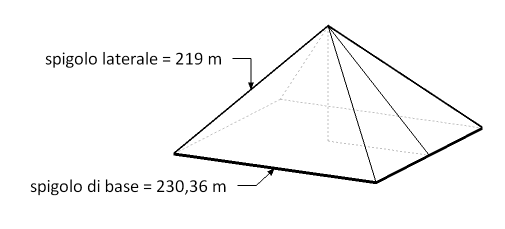
Il numero di nodi per ogni lato è una terna pitagorica, cioè tre numeri che possono essere pensati come la misura dei lati di un triangolo rettangolo.
ENUNCIATO DEL TEOREMA
Oltre al caso particolare del triangolo rettangolo isoscele (quello del pavimento osservato da Pitagora) abbiamo considerato un caso più generale:
Sui cateti
a e
b e sull'ipotenusa
c sono stati costruiti dei quadrati.
Le aree di questi quadrati sono quindi
a^2,
b^2, c^2.
Abbiamo preso un triangolo rettangolo di cateti
a e
b ed abbiamo costruito un quadrato di lato
l=a + b.
Abbiamo suddiviso il quadrato come nella figura a destra, in 4 triangoli rettangoli di cateti a e b ed un quadrato (azzurro) costruito sull'ipotenusa di questi triangoli. Poi abbiamo ricombinato il quadrato come nella figura a sinistra, cioè in 2 rettangoli (gialli) fatti ciascuno da 2 triangoli gialli, mentre la parte restante del quadrato di lato l=a + b è costituita da due quadrati azzurri di area a^2 e b^2.
L'area del quadrato di lato
l=a + b può essere espressa così in due modi:
AQ= 4xT + c^2 (figura a destra)
AQ= 4xT + a^2 + b^2 (figura a sinistra)
Dunque:
4xT + c^2
= 4xT + a^2 + b^2
da cui
c^2= a^2 + b^2
ENUNCIATO
In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è sempre equivalente alla somma dei quadrati costruiti sui cateti.
Puoi anche dire:
In ogni triangolo rettangolo l'area del quadrato costruito sull'ipotenusa è sempre uguale alla somma delle aree dei quadrati costruiti sui cateti.
Vuoi rivedere le
terne pitagoriche, cioè a quelle terne di numeri interi che soddisfano il teorema di Pitagora?
Leggi qui:
http://bredainrete.blogspot.it/2015/01/2a-terne-pitagoriche.html
Alcune terne pitagoriche:
3, 4, 5 Derivate: 6, 8, 10 - 9, 12, 15 - 12, 16, 20 - 15, 20, 25 - 18, 24, 30 - 21, 28, 35 - 24, 32, 40 - 27, 36, 45 - 30, 40, 50
5, 12, 13 Derivate:10, 24, 26 - 15, 36, 39 - 20, 48, 52 - 25, 60, 65
7, 24, 25 Derivata: 14, 48, 50 - 21, 72, 75 - 28, 96, 100
8, 15, 17 Derivata: 16, 30, 34 - 24, 45, 51
9, 40, 41 Derivata: 18, 80, 82
12, 35, 37 Derivata: 24, 70, 74
11, 60, 61